Combinations vs Permutations
Classical combinatorics (Pascal, Newton and successors)
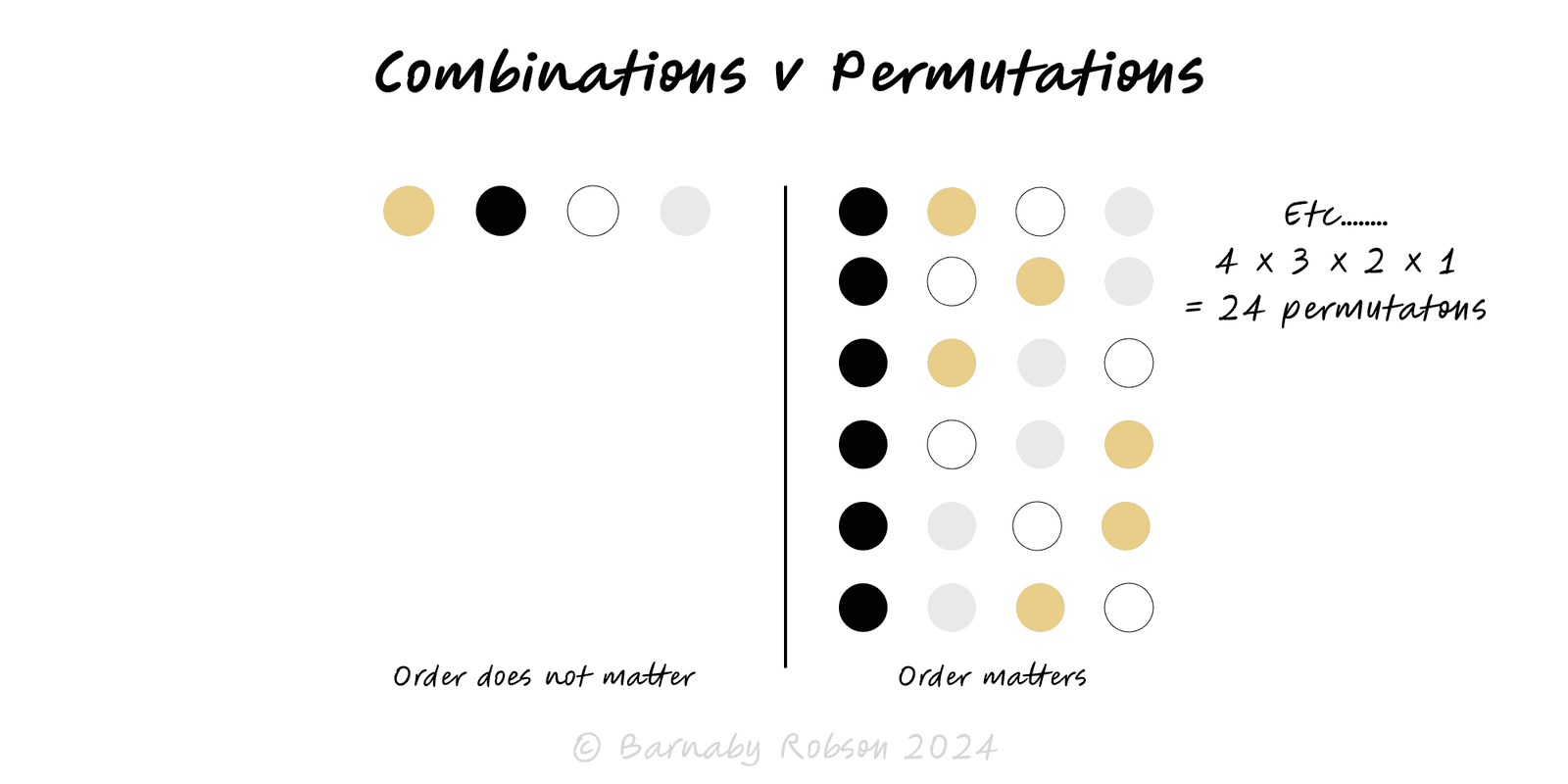
Counting outcomes underpins probability, testing and design choices. Permutations count ordered selections; combinations count unordered selections. The right choice depends on two questions: (1) does order matter? (2) can you reuse items (replacement)? Getting this right prevents over/under-counting, bogus probabilities and wrong sample sizes.
Notation & basics
- Factorial: n!. Falling factorial: n(r) = n!/(n−r)!.
- Permutations (order): P(n,r) = n!/(n−r)!.
- Combinations (unordered): C(n,r) = n!/[r!(n−r)!].
- Link: P(n,r) = C(n,r) × r! (each unordered set can be ordered in r! ways).
The four common cases
| Order matters? | Replacement? | Count | |
|---|---|---|---|
| 1 | Yes | No | P(n,r) = n!/(n−r)! |
| 2 | Yes | Yes | n^r |
| 3 | No | No | C(n,r) = n!/[r!(n−r)!] |
| 4 | No | Yes | C(n+r−1, r) (combinations with repetition) |
Quick intuition
- If you’d treat “ABC” and “CBA” as different, use permutations.
- If “ABC” and “CBA” are the same group, use combinations.
- Replacement allowed? Think PIN codes (can reuse digits) vs lottery balls (without replacement).
Product & ops – SKU/option explosion, menu design, routing/scheduling possibilities.
Research & testing – number of test variants, multi-factor designs, sample-space sizing.
Security – password/PIN complexity, keyspace sizing.
Hiring & teams – ways to assign roles, select panels or rota patterns.
Risk & probability – lottery odds, card draws, defect sampling (hypergeometric vs binomial).
Define items and r – “Choose r from n”. State any caps or must-include rules.
Decide order – does arrangement change meaning? If yes, use permutations.
Decide replacement – can an item repeat? If yes, use the replacement versions.
Write the formula – pick from the 4-case table; simplify algebraically.
Sanity-check – test extremes (r = 0, r = 1, r = n) and small n with manual enumeration.
Add constraints – if there are exclusions (e.g., “at least one vowel”), use inclusion–exclusion or break into cases.
For large n – use log-factorials / Stirling’s approximation to avoid overflow; or simulate to validate.
Worked mini-examples<
Team selection: choose 3 judges from 10. Order doesn’t matter, no replacement → C(10,3) = 120.
Podium outcomes: gold–silver–bronze from 10. Order matters, no replacement → P(10,3) = 720.
3-digit PIN: digits 0–9, order matters, replacement allowed → 10³ = 1000.
Scoops with repeats: 3 scoops chosen from 5 flavours, order irrelevant, repeats allowed → C(5+3−1,3) = C(7,3) = 35.
Dividing (or not) by r! incorrectly – causes ×r! errors.
Forgetting replacement rules – using n^r when items can’t repeat, or P/C when they can.
Hidden constraints – “no adjacent duplicates”, “at least one from X” change the count.
Indistinguishable items – identical objects require stars-and-bars or partition methods, not plain P/C.
Over-relying on averages – probability conclusions fail if the sample space was miscounted.
