Game Theory
John von Neumann & Oskar Morgenstern; John Nash; many successors (Aumann, Schelling, Myerson)
Game theory studies interdependent decisions. Players choose strategies; payoffs depend on everyone’s choices. An equilibrium (often Nash) is a stable profile where no player wants to deviate on their own. The craft is twofold: (1) analyse the given game to predict behaviour; (2) change the game—payoffs, information, or timing—so better outcomes become equilibrium.
Game type – zero-sum (one’s gain is another’s loss) vs non-zero-sum (scope for win–win or traps).
Information – complete/incomplete; perfect/imperfect; simultaneous vs sequential moves.
Equilibria – Nash (no unilateral gain by deviating), subgame perfect (credible in every subtree), mixed strategies when no pure equilibrium exists.
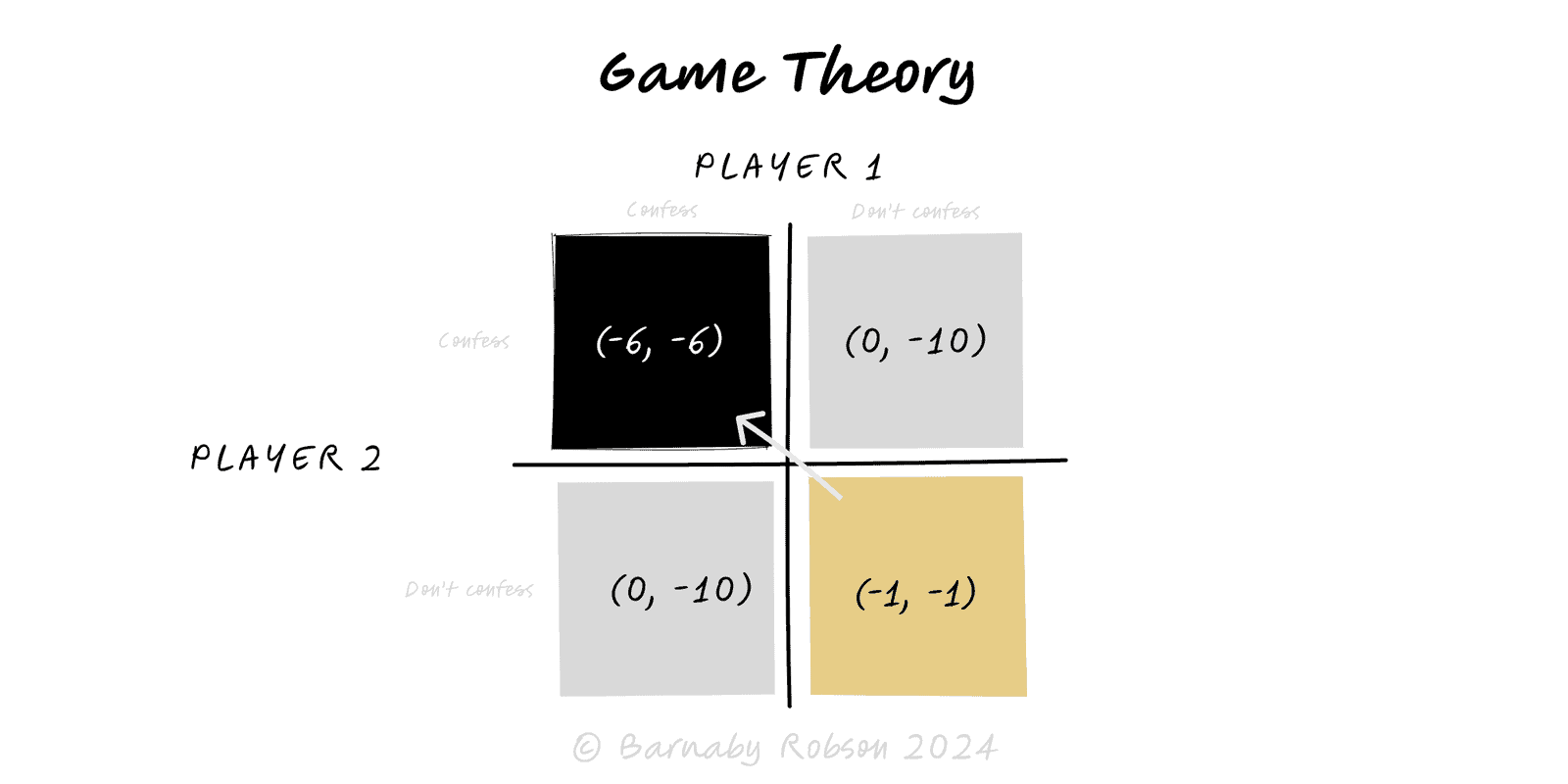
Canonical games – Prisoner’s Dilemma (co-operation trap), Stag Hunt (coordination & trust), Battle of the Sexes (coordination with preference conflict), Matching Pennies (zero-sum).
Dynamic effects – repeated games enable reputation, reciprocity, and trigger strategies; signalling/screening convey or extract private information; commitment and credible threats reshape incentives.
Mechanism design – set rules/contracts/auctions so participants’ incentives produce the outcome you want.
Game type – zero-sum (one’s gain is another’s loss) vs non-zero-sum (scope for win–win or traps).
Information – complete/incomplete; perfect/imperfect; simultaneous vs sequential moves.
Equilibria – Nash (no unilateral gain by deviating), subgame perfect (credible in every subtree), mixed strategies when no pure equilibrium exists.
Canonical games – Prisoner’s Dilemma (co-operation trap), Stag Hunt (coordination & trust), Battle of the Sexes (coordination with preference conflict), Matching Pennies (zero-sum).
Dynamic effects – repeated games enable reputation, reciprocity, and trigger strategies; signalling/screening convey or extract private information; commitment and credible threats reshape incentives.
Mechanism design – set rules/contracts/auctions so participants’ incentives produce the outcome you want.
Define the game – players, feasible actions, timing, what each player values (payoffs).
Build the model – 2×2 payoff matrix (simultaneous) or extensive-form tree (sequential with information sets).
Solve
Eliminate strictly dominated strategies.
Best-response reasoning to find Nash equilibria (use backward induction for sequential games → subgame perfect).
If none in pure strategies, compute mixed (randomised) equilibria.
Stress the assumptions – are payoffs right? what is common knowledge? is the move order accurate?
Change the game
Commit (contracts, capacity, pricing guarantees).
Shift payoffs (carrots, penalties, side-payments, reputation effects).
Change information (signalling, screening, transparency).
Repeat the interaction to support co-operation with trigger strategies.
Pilot & measure – run small tests; watch behaviour, not just stated preferences; iterate the model.
Wrong payoffs – pretty maths with the wrong incentives predicts nothing.
Static when dynamic – solving a one-shot game that is actually repeated.
Incredible threats – strategies that won’t be optimal when the moment arrives (fix with subgame perfection or commitment).
Equilibrium selection – multiple equilibria; use focal points, small frictions, or coordination devices.
Misreading mixed strategies – they model unpredictability, not indecision; often implement as controlled randomisation.
Over-engineering – mechanisms too complex for humans or systems create new failure modes.